where n is a unit outward normal on
A continuous body is usually deformed in the laboratory either by applying a
distributed load on a part of its boundary and/or by specifying displacements
on another part of the boundary. For example when a bar is pulled in a
universal testing machine, one end of the bar is kept fixed and the other is
pulled either at a prescribed rate or with an assigned force. Thus
displacemets are prescribed to be zero at the fixed end, surface tractions
equal zero on the lateral surface of the bar, and either displacements or
tractions are prescribed at the other end. Whereas we usually represent force
at the pulled end by a point load, in continuum mechanics (which includes
elasticity, plasticity, fluid mechanics etc.) only distributed forces
are considered. Let ![]() and
and ![]() represent
complementary parts of
the boundary of
represent
complementary parts of
the boundary of ![]() . The boundary conditions are expressed as
. The boundary conditions are expressed as
![]()
where
n is a unit outward normal on ![]() , and
, and
![]() and fi are given functions of
x1,x2,x3 on the boundary of
the body. The left-hand sides of (7.1) and (7.2) represent limiting values of
the displacement and surface tractions at a point on the boundary
as that point is approached from the
interior of the body, and the right-hand sides are the prescribed values.
f is called surface tractions and has the units of stress or
force/area.
and fi are given functions of
x1,x2,x3 on the boundary of
the body. The left-hand sides of (7.1) and (7.2) represent limiting values of
the displacement and surface tractions at a point on the boundary
as that point is approached from the
interior of the body, and the right-hand sides are the prescribed values.
f is called surface tractions and has the units of stress or
force/area.
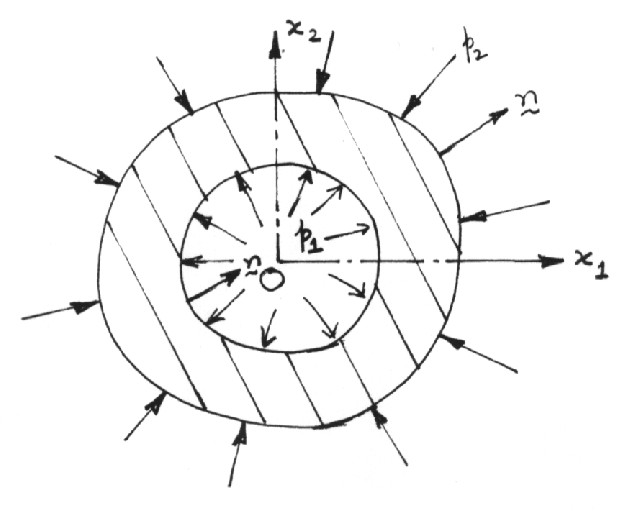
The boundary conditions at the inner and the outer surface of a cylindrical
pressure vessel subjected to an internal pressure p1 and external pressure
p2 are expressed as (see Fig. 7.1)
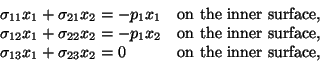 |
(7.5) |
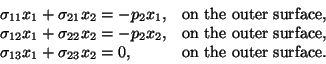 |
(7.6) |
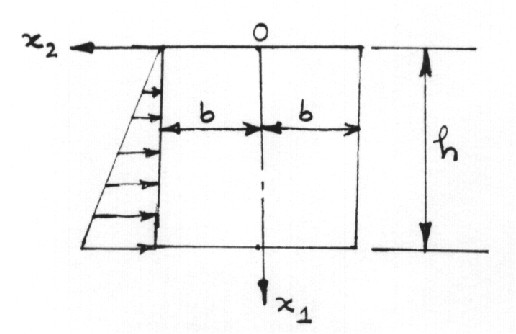
For a long prismatic dam (see Fig. 7.2)
subjected to water pressure that increases linearly
with the depth, the boundary conditions are as follows.