Generalized Plane Strain FEM Problem: NPIB

Submit batch job to compute stresses in a [0/90/45/-45]s "Type-II"
Graphite/Epoxy laminated composite plate with a ply-crack

Instructions for using this form:

    1. Enter appropriate numbers in the boxes,
    2. enter your email address,
    3. click on submit, and
    4. wait for results to be returned to your email. (this will take about 20 seconds)
  1. Web location of results: pc4l.html will be sent to your email address.
  2. If your email does not provide direct email links, copy and paste the web address: http://www.jwave.vt.edu/output/pc4l_"unique date-time"/pc4l.html from the email into your web browser Location: window and look at this file to see if the job ran correctly.
  3. If the job ran correctly you can now download files from your web browser to your computer for archiving (a 4.6Gbyte read/write optical disk is available for each student to use in the SMVC for archiving large simulation files).
  4. If you submit the form "as-is", a sample of results has been archived in the directory: http://www.jwave.rkriz.net/output/ARCHIVE_Examples_SAVE/pc4l_10-23-2000-8:39:55:361/
    Select pc4l.html to see a summary of the results.

Below is a description of the laminate geometry and finite element grid representation used to define the "4-Layer Ply-Crack" problem. A detailed explanation of the "4-Layer Ply-Crack" problem is given in Ref.[17],"Influence of Ply Cracks on Fracture Strength of Graphite/Epoxy Laminates at 76K", ASTM STP836, (1984), describes an actual application using this computer program for the reader. As a summary the figures below shows the laminate stacking sequence, FEM grid, and stress distributions for this specific problem. Example of results shown below demonstrate how a ply crack influences the stress distribution along the laminate 0/90 interface and through the 0 degree ply near the ply crack tip.

Notice how the sigma-z sigma-hz and sigma-h stresses are influenced by thermal ("THERM") and moisture ("MOIST") conditions supperposed with the mechanical ("MECH") load case. These three stress distributions are significantly influenced by the combination of residual stresses caused by the thermal contraction at low temperatures, Delt-T=-180F, and swelling caused by moisture absorbtion, Delt-M=1.2% moisture, such that the ply crack can be controlled to either grow into the adjacent load bearing 0-degree ply ("WET") or delaminate along the 0/90 interface ("DRY"), see Figures 4 and 5.


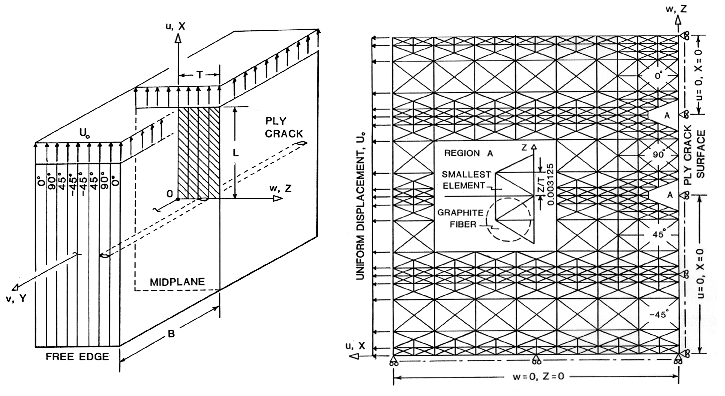
Figure 1. Schematic and FEM grid of a ply crack in a [0/90/45/-45]s Laminate


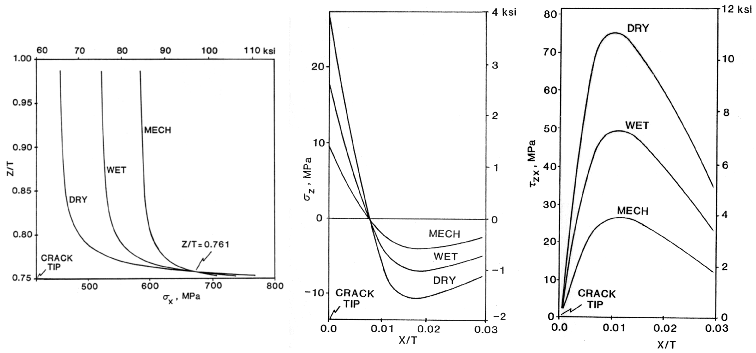
Figure 2. Mode-I stresses in the 0 degree load bearing ply above the ply crack

Numbers provided in the NPIB (Network Programming Interface Builder) form below match this particular problem. Of course with the NPIB form a variety of other configurations are possible.

NOTE: We have provided a complete set of ELEMENT NUMBER GRIDS below so that the student can calculate stress distributions different from the three graphs shown above.

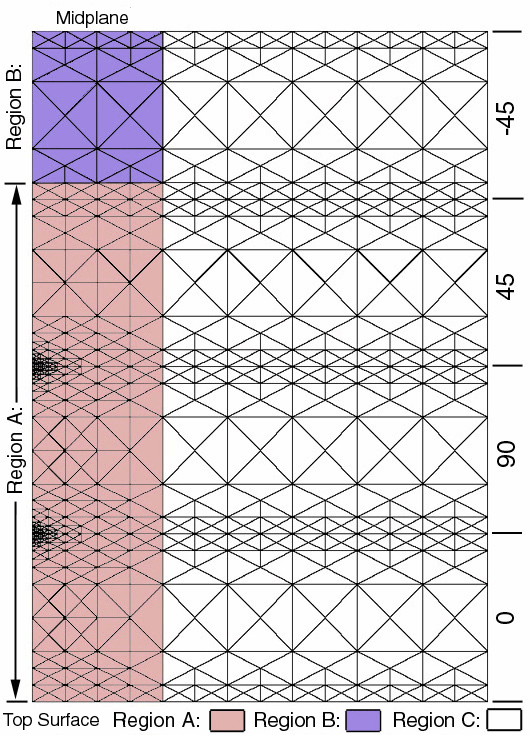Region-A     / Region-B     / Region-C

You might want to reproduce the results shown in th figures above using the form in the frame provided below. You will also need to use the Linear Elastic Laminated Plate Analysis (LELPA) program in "module08" which is used to convert the Nx=1552 lb./in. into strains in the x and y directions. The strain in the y-direction, calculated by LELPA, is then used as the out-of-plane strain normal ("N-direction") to the H-Z plane in the form below. The strain in the x-direction ("H-direction") is imposed by nodal displacements.